1. I Walk the Line♭Johnny Cash 1957: Linear Algebra

    Matrices play very important roles in many economic theories, and one key application of them is to solve linear systems of equations. This might sound like high school algebra or that it applies only to very simple economic models. But linear systems are almost always embedded in dynamic, non-linear models. So they underly many if not all sophisticated economic theories. A clear notion of how to handle linear systems numerically is essential for doing numerical economics, even if knowing the details of the algorithms is not important. First, let's ensure we all agree on names for kinds of matrices.

  1. A Review of Matrices and Linear Algebra
    CW 4.1-4.6
    2. A real matrix $A$ has element $a_{ij}$ in row and column $j$. We can define a matrix using a formula for the elements. So $A_{n\times m} = [ a_{ij} ]$ means "$A$ is the $n\times m$ matrix with elements $a_{ij}$." This is a compact way of writing $$A = \l(\matrix{ a_{11} & a_{12} & \cdots &a_{1m} \cr a_{21} & a_{22} & \cdots & a_{2m}\cr \vdots & \ddots & \cdots & \cr a_{n1}& a_{n2} &\cdots& a_{nm}}\r).\nonumber$$ For example, $A_{2\times 3} = [ i-j ]$, then $A = \l(\matrix{0&-1&-2\cr 1 & 0 & -1\cr}\r).$ Given the notation above to describe a matrix we can define special matrices simply.
    "$A$ is square" means … $n=m$.
    When $n=1$ we say … "$A$ is a row vector."
    When $m=1$ we say … "$A$ is a column vector."
    When $i \lt j \rightarrow a_{ij}=0$ we say … "$A$ is lower triangular."
    "$A$ is diagonal" means … $i\ne j \rightarrow a_{ij}=0$.
    When $n=m$ and $a_{ij}=a_{ji}$ we say … "A is symmetric."
    "$A = I$" means $n=m\ \&\ a_{ij}=\cases{ 1 & i=j \cr 0 & $i\ne j$\cr}$
    Given two arbitrary matrices, $A_{n\times m} = [a_{ij}]$ and $B_{r\times s} = [b_{ij}]$, and two arbitrary column vectors of the same length, $v_n = [v_{i}]$ and $y_n = [y_{i}]$, we can define most of the key matrix operators.
    Transposing a matrix swaps rows and columns: $A' \equiv [a_{ji}]$. So if $A= \l(\matrix{1&2&3\cr 4&5&6\cr}\r)$ then $A' = \l(\matrix{1&4\cr 2&5\cr 3&6\cr}\r).$
    Summing two matrices creates the matrix of corresponding elements added together: $A+B \equiv \left[a_{ij}+b_{ij}\right]$, which requires $n=r, m=s$. So $$\l(\matrix{1&2\cr 3&4\cr}\r)+\l(\matrix{-1&0\cr -1&0\cr}\r) = \l(\matrix{0&2\cr 2&4\cr}\r).\nonumber$$
    Matrix multiplying two matrices is the sum of the multiplication of left-hand rows with right-hand columns. $AB \equiv \left[\sum_{k=1}^m a_{ik}b_{kj}\right]$ which requires the inner dimensions to be equal: $m=r$. $A= \l(\matrix{1&2&3\cr 4&5&6\cr}\r)$, $B= \l(\matrix{1&-1\cr 1&-1&\cr 1&-1\cr}\r)$ then $$AB = \l(\matrix{6&-6\cr 15&-15\cr}\r).\nonumber$$
    The dot or inner-product of two vectors is like matrix multiplication, but it is defined for vectors of the same size using matrix transpose: $v \circ y \equiv v'y = \sum_{j=1}^n v_{j1}*y_{j1}$, which requires $n=r, m=s=1$.
    The norm of a vector $v$ is a notion of its size: $\|v\| \equiv \sqrt{v\circ v} = \sqrt{\sum_{i=1}^n v_{i}^2}.$ So $v = \l(\matrix{1\cr -1\cr 2}\r)=\sqrt{6}.$
    $A\ .\circ B = \left[ a_{ij}b_{ij}\right]$, which requires $n=r, m=s$. This is a dot-operator or element-by-element operator. Dot operators in Ox are written just like that: .*, ./, etc.
  2. Determinant and Inverse of Square Matrices
    3. $\det\{A\}$ or $|A|$ is a function $\Re^{n\times n}\to \Re$ as:
    When $n=1$ the matrix is simply a number, $A = (a_{11})$. And its determinant is that number: $|A| = a_{11}$.
    When n=2 the determinant is the familiar formula $|A| = a_{11}a_{22}-a_{21}a_{12}$. Notice this is the sum of two products, each multiplying two elements of the matrix.
    When $n=3$ the determinant is $+/-$ 6 products of 3 matrix elements.
    In general $|A| = $ sum of products of $n$ elements of $A$. That is, the determinant is a nth order polynomial in the elements of $A$. So there are $n$ roots to an equation that sets $\det(A)=0$, allowing for repeated and complex roots.
    $A^{-1}$ is the matrix which, when multiplied by $A$, results in the identity matrix: $A^{-1}A = AA^{-1} = I_n$.
    This is the matrix concept of division. Only square matrices have well-defined inverses like that, although generalized inverses are defined for non-square matrices.
    As you probably remember, the determinant of a square matrix is a single number that summarizes many of its important properties, including whether $A^{-1}$ exists.

    Table 11. Basic Matrix Operators in Ox 

    Name         Symbol           In Ox           Example Code
--------------------------------------------------------------------------------
Transpose    ′                ′                B = A';
Sum          +                +               C = A + B;
Multiply                      *               C = A*B;
Dot Product  ∘                ′*              h = v′*y;
Norm         || ||            norm()          h = norm(v,2);
Determinant   | |             determinant()   h = determinant(A);
Inverse       -1            -1            B = A^(-1);
                              /               B = 1 / A;
                              invert()        B = invert(A);
  3. Linear ≡ Easy
    KC p. 106
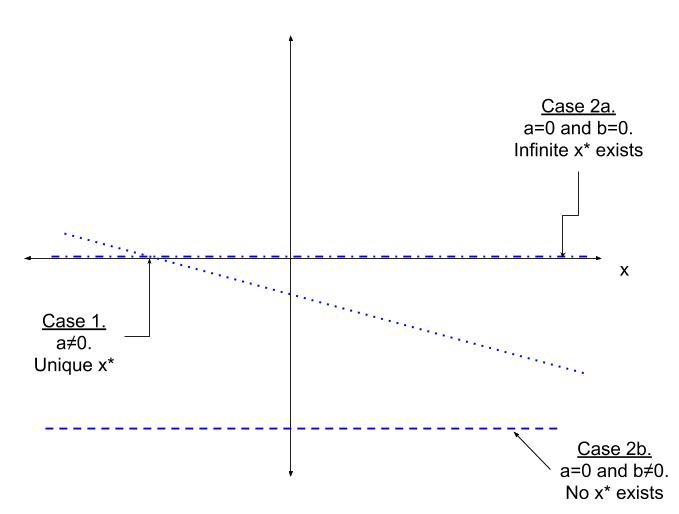
    4. One of the conveniences of linear systems is that the dimension of the system does not alter the basic notions. Most of what can be said for square $n\times n$ linear systems is a direct analogue to what can be said of a scalar $1\times 1$ system. A scalar linear system can be written $$ax = b,\nonumber$$ where $a$ and $b$ are given real numbers and $x$ is an unknown quantity. This system has a unique solution for $x$, $b/a$, as long as $a\ne 0$. Another way to write $b/a$ is $a^{-1}b.$ For example, $2.2x = -0.2$, then $x = (2.2)^{-1}(-.2) = -.011$.

    If $a=0$ then the system is not invertible and is said to be singular. There are two possibilities depending on $b$. If $b = 0$ as well then any value of $x$ is a solution to the system ($0x=0$), so instead of one solution we get an infinite number of solutions (any value works). If $a=0$ but $b\ne 0$ then there is no solution to the system.

    Exhibit 32. Scalar Linear Systems: 3 Possibilities

    So in a scalar linear system there are either 0, 1 or infinite values of $x$ that solve the system. Which case applies depends first on a single number, $a$, and if $a=0$ then the value of $b$ also matters. When we generalize to $n$ dimensional linear systems, the only difference is what number plays the role that $a$ does in the scalar system. You know this number as the the determinant of the matrix.

    Definition 2. All Possible Cases of Linear Systems

    Given $A$ ($n\times n$) and $b$ a $n\times 1$ column vector, is there an $x$ vector such that $$\mathop{A}\limits_{_{n\times n}}\ \mathop{x}\limits_{_{n\times 1}} = \mathop{b}\limits_{_{n\times 1}}?\nonumber$$
    1. When $A$ is invertible
            «No row of $A$ is a linear combination of the other rows»
      $\Leftrightarrow\quad$ «No column of $A$ is a linear combination of the other columns»
      $\Leftrightarrow\quad$ «$|A| \ne 0$»
      $\Leftrightarrow\quad$ « $!\exists A^{-1}: A^{-1}A = I$»
      $\Leftrightarrow\quad$ «$!\exists\ x= A^{-1}b$»
    2. When $A$ is not invertible
           «At least one row of $A$ is a linear combination of the other rows»
      $\Leftrightarrow\quad$ «At least one column of $A$ is a linear combination of the other columns»
      $\Leftrightarrow\quad$ «$|A|= 0$»
      $\Leftrightarrow\quad$ «$\not\exists A^{-1}$»
      $\Leftrightarrow\quad$ «$b\ne 0\ \Rightarrow\ \not\exists\ x: Ax = b.$»
      $\Leftrightarrow\quad$ «many $x$ satisfy $Ax=0$ (called the null space of $A$).»
    In standard mathematics for economics textbooks the solution to linear systems is connected directly to finding the inverse of $A$: $$x = A^{-1}b.\nonumber$$ Alas, the computationally efficient method to solve the system does not rely on matrix inversion. In fact, the reverse is true: matrix inversion relies on solving linear systems.