We used processing of vectors and matrices to introduce for () loops. In particular, adding two matrices together using scalar addition uses two nested loops, the outer loop goes over the row index $i$ and the inner loop goes over the column index $j$. A for or foreach loop makes sense because the number of trips each loop takes is given.
This section introduces the notion of convergence of an iterative process. Each step of the process works on the output or result of the previous step. The process continues until the next step is not different than the last, which means the process has converged. The number of iterations is not fixed ahead of time (in contrast of for loops over the dimensions of a matrix). This is a natural application of a while() or do while() loop.
- A Simple Dynamic System
- Converging to a Steady-State
/** iterate(f,x0,toler=1E-8) f : function of the form f(xt), the process to iterate on, xt+1 = f(xt) x0 : initial value toler : tolerance for convergence **/ iterate(f,x0,toler) decl x_tod, x_tom, done; x_tod = x0; // do while() version done=FALSE; do { while(!done) { x_tom = f(x_tod); x_tom = f(x_tod); done = isfeq(x_tom,x_tod,toler); done = isfeq(x_tom,x_tod,toler); x_tod = x_tom; x_tod = x_tom; } } while (!done); return x_tod; }
Notice that this function takes another function as an argument. That is, you can send a function as input to another function. This allows a general purpose algorithm to be coded that works not just on different input variables but also "operates" on a function chosen by the user. In Ox, to pass a function to a function you simply give the name of the function. For example, suppose $f(x)=\sqrt{x}.$ Since this is a built-in function you can just send it to iterate(sqrt,2.0,1E-8);
You do not include - A Discrete Markov Process The example above illustrates the basic idea of an iterative process with the simplest case of a single value $x_t.$ This is sometimes called a state variable and the function $f(x_t)$ is called the transition or the law of motion. Different jargon is used in different contexts, but the basic idea is the same.
- Verifying a Matrix Satisfies Constraints
- Following a Markov System
- Norm of a vector
Think about a value $x$, such as GDP of a model economy. It could be the population of a species, or other the spread of virus, but we'll stick with GDP. A dynamic model for $x$ says that next period's GDP is a function, $f(x),$ of the current GDP. (A theory might make $f()$ depend on things like savings rate and technology. For our purposes we just start with $f(x)$ not the economics behind it.)
Let $t$ denote time, so $x_t$ is the value of $x$ in period $t$. Any dynamic model has initial conditions that are determined outside the model. In this case, we start the economy at some GDP level, $x_0.$ The model says next period's value is a function of this period: $$x_{t+1} = f(x_t).$$ This is a simple dynamic process. We could use this process to trace out the path of the economy: $$x_4 = f(x_3) = f( f(x_2) ) = f( f( f( x_1))) = f(f(f(f(x_0)))).$$ But we can also ask is there a point in which the path gets to a point when the economy just becomes constant. That is, is there a value $x^\star$ such that $$x^\star = f(x^\star).$$ That means that if the level of GDP the economy ever gets to $x^\star$ it is the same size forever. We say that $x^\star$ is a steady-state of the economy, and if we can start at some $x_0$ and reach $x^\star$ we say that the process $x_{t+1}=f(x_t)$ converges to $x^\star$.
First, let's think about a process that does not converge. Suppose $f(x) = e^x.$ Then this economy experiences exponential growth. Each period GDP is higher than the next and the economy's GDP is unbounded. Thus, no matter what $x_0$ we start at $x_t$ just keeps going towards $\infty.$ This would be a case we would say this process never converges (or it diverges). You can plot this on a simple graph.
On the other hand, suppose $f(x) = 1+\ln(x).$ This economy will grow when $x$ is small. If we start at a low value, $x_0$, then $x_1 = 1+\ln(x_0)$ will be larger than $x_0$. However, if we start with a very large $x_0$ then $x_1$ will be smaller than $x_0$ because $1+\ln(x) \lt x $ is $x$ is big enough. There is a value $x^\star$ such that $1+\ln(x^\star) =x^\star.$ (There might be more than one value that is a steady-state.)
Exhibit 31. Convergence or Divergence of a Simple Iterative Process
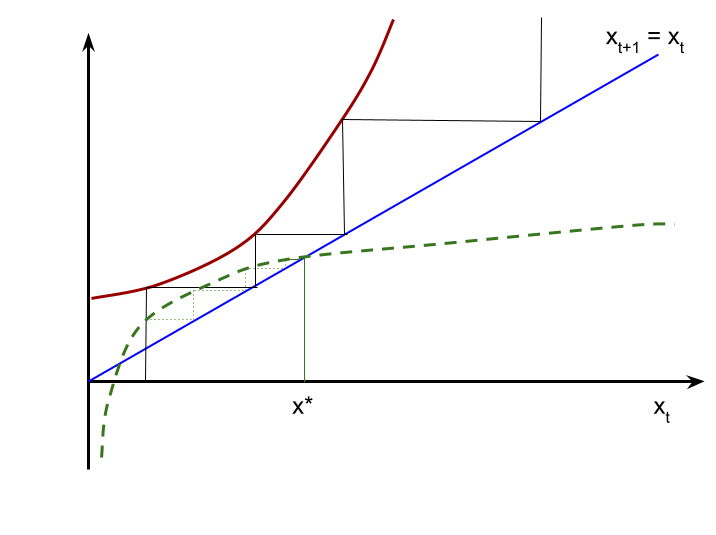
There are different ways to try to find the steady-state of some process. We want to use it as an example of an iterative process converging, which is a basic idea that we see multiple times in this class. For now let's assume $x^\star$ exists and, unlike exponential growth, the dynamic system does not converge. Then to find $x^\star$ e could starting at some $x_0$ and iterating on $x_{t+1} = f(x_t)$ until $x_t$ gets to $x^\star.$ This is a simple loop. Note that we would be storing $x_t$ as a FPR, so there is no guarantee we can ever get the difference to exactly 0, because $x^\star$ might not even be a FPR. And even if we can get to it exactly it might not be necessary to iterate until the difference is exactly 0. So, instead, we should continue until $x_t$ is close enough to converging, which means $|x_{t+1} - x_t|$ is small. A while loop could keep going so long as $|x_{t+1}-x_t| > \epsilon,$ where $\epsilon$ is a tolerance level chosen by the user or the coder.
We already saw tthe Ox function isfeq(a,b,fuzziness), which would check for convergence. Here fuzziness is an optional argument that is the $\epsilon$ to use. It should be set equal to something larger than machine precision, which is approximately $10^{-16}.$ For example, the square root of machine precisions is $\epsilon = 10^{-8}$ is still small but means we can report $x^\star$ to at least 6 decimal digits of accuracy. That might be "close enough" for our purposes.
This is the basic idea of any "iterative" solution method: set an initial value and keep iterating until the process converges to some level of tolerance. Here is a function that is a template for this procedure.
iterate()
( ) or (x) when passing a function. That would call the function and then pass its return value. You simply provide it's name.
If you want to iterate on $f(x) = 1 + \ln(x)$ then you would code the function and send the name of the function to iterate(). (Ox has "anonymous" functions like other languages which would allow you to define the function in the call to iterate, but we avoid using that syntax for simplicity.)
Two different loops are shown that do the same thing. One use a while() loop, which checks the condition at the "top." This kind of loop has to have initial conditions set before the first pass of the loop. So done is set to FALSE to fall into the loop the first time. The other version is a do while() loop in Ox, which puts the check to continue at the bottom of the loop. This structure guarantees the body of the loop has to happen at least once. Since the condition to check is determined inside the loop all that is necessaary to initialize is the initial value of x_tod. Notice x_tom is computed using the function passed as f. Then the difference between today's and tomorrow's values is checked. Only then does either loop copy tomorrow into today's value so that it will be used the next time round. This is the equivalent of the horizontal lines going from $f(x_t)$ to the diagonal line.
A Markov process describes this basic idea: that the state of the system in the next period is a function of the previous state or situation. A discrete Markove process is a case when the system is in one of a finite number of discrete states. So instead of thinking of a continuous variable like GDP, think of two states: either a contraction (0) or an expansion (1). The economy is in one of these states each period. Next period it either stays in the same state or it moves to the other one. So a recession is a number of consecutive contractions before the state switches to expansion. You can think of bear and bull markets as another case. Or a person might be employed or unemployed. These are each two state models, but there can be, say, $J$ different states. For example, unemployed, in school, working part-time, working full-time, and retired might be a five state model of a person's labour market status.
So if the system can be $j$, one of $J$ states, there is a transition that gives the probability the system is in each of the $J$ states next period. For each $j$ there are $J$ transitions, so a transition is a $J\times J$ matrix. So if the current state is $j$, then $p_{ij}$ is the probability that the system is in state $i$ next period. Think of $p_{0j}$, $p_{1j}$,$\dots$,$p_{J-1\,j}$ as a column vector. Put each of these column vectors into matrix $P$ and you have the transition. So, whatever $j$ is, each value of $p_{ij}$ has to be in the range $[0,1]$ because it is probability. And the probabilities have to add to $1$: $$ p_{ij}\ge 0\qquad \hbox{and } \sum_{i=0}^{J-1} p_{ij} = 1 \hbox{ for all } j.$$ Note that if each element of $P$ is greater than or equal to 0 and each columns sums to 1 then we don't have to also check that each element is less than or equal to 1.
How could we verify a matrix $P$ satisfies those conditions and is thus a valid transtion? Here is one way using two nested loops: the outer loop goes over columns; the inner loop goes over the rows of the current column to make sure they satisfy the conditions above. First, initialze a variable (maybe called valid) to be TRUE. Then inside the inner loop if any element of $P$is less than 0 set valid to FALSE. (You could quit the loops then using break discussed earlier). And simply add up the values in the current column using the "sum of a vector" code. If any column sum is not fuzzy equal to 1.0 then again set valid to FALSE. If you get through all the columns and valid is still TRUE then $P$ is a valid transition matrix.
But, return to section on matrices that discussed functions and operators (or Ox documentation it is drawn from). Any logical operator like the > operator can used with matrices or a matrix and number. THey always return either TRUE or FALSE for all comparisons of the elements of the matrices involved. This is different than the "dot" versions such as .> which returns a matrix of true and false values. So if $A$ is a matrix then A >= 0 equals TRUE if all elements of $A$ are greater than or equal to 0. You do not need to use a loop to check equal element separately. There is also a very useful function, sumc(A) which returns the sum of columns of the matrix $A$ as a vector. Your code can then ask if that vector of column sums is fuzzy equal to 1.0. In other words, the conditions for a valid transition matrix can be checked with a very simple expression.
How do let a discrete Markov system play out like the simple growth model iteration? As with any dynamic system initial conditions have to be given. Suppose we start the system in discrete state $j,$ for example in a recession. Then let $f^0$ be $J\times 1$ vector with 0s and a single 1 in the $j^{th}$ row. So if $f^0_2=1$ it means that the system is in state 2 in the initial period $t=0$. The 0s in the other elements mean it is not in the other states.
What happens next period $1$? Simply pre-multiply $f^1$ by $P$: $$f^{1} = P f^0.$$ This new $J\times 1$ vector equals the column of $P$ corresponding to the state that has the 1 initially. We don't know which state the system will be in in $t+1$, just the distribution across states. In general, if we know the distribution over states in time $t$ and it is stored in the column vector $f^t$, then next period the distribution is $$f^{t+1} = Pf^t.$$ This is another iterative process just like the growth models above. We could track the distribution over time to see how the system evolves. But just like the growth model, we might ask is there a steady-state of the system? That is, is there a distribution over states $f^\star$ such that $$f^\star = Pf^\star?$$ This does not mean the system doesn't change. If we followed the system it is always in a particular state each period. But if the distribution $f^\star$ satisfies that condtion then the distribution over states is the same next period and every period thereafter. This is called the stationary or ergodic distribution of the system.
Just like above, we can iterate on this Markove process until the distribution is close enough to the stationary distribution. But now $f^{t+1}$ and $f^t$ are not single numbers. They are vectors. The stationary distribution is the case when the So we need a measure of distance between two vectors. In the case of the scalar $x$ we could simply look at $|x_{t+1}-x_t|$. One measure of distrance is Euclidean distance: $$d(f^{t+1},f^t) = \sqrt{\sum_{i=0}^{J-1} (f^{t+1}_i-f^t_i)^2}.$$ If $J=1$ then this measure of distance simplifies to the absolute value. of the difference just like in the growth model. So now the decision to stop the iteration is if the distance is small enough.
TO BE COMPLETED