1. Search

    Modern economics incorporates incomplete information and market frictions into the model of decisions. (In contrast, the utility maximization and Edgeworth Box applications include full information and smoothly working markets.) One of the simplest and most widely applied cases of this is the sequential search model.

  1. Basic Set Up
    2. Consider a Queen's student Jean who is looking for their first job. We will start with a very stylized model that leaves out lots of details in a real job search in order to capture a main effect. First, suppose Jean accepts a job that pays $w$ each period. (A period might be a month so $w$ is earnings on the job each month.) An accepted job lasts forever at a constant wage, and Jean values that in terms of its present discounted value: $$v_1(w) = {\sum}_{t=0}^\infty \delta^t w = w(1+\delta+\delta^2+\cdots) = {w\over 1-\delta}.$$ Here $\delta$ is Jean's discount factor. The subscript "1" is used because this is value of acceptance which can code as setting a variable $a=1.$ The other option Jean has is to reject a job offer ($a=0$).

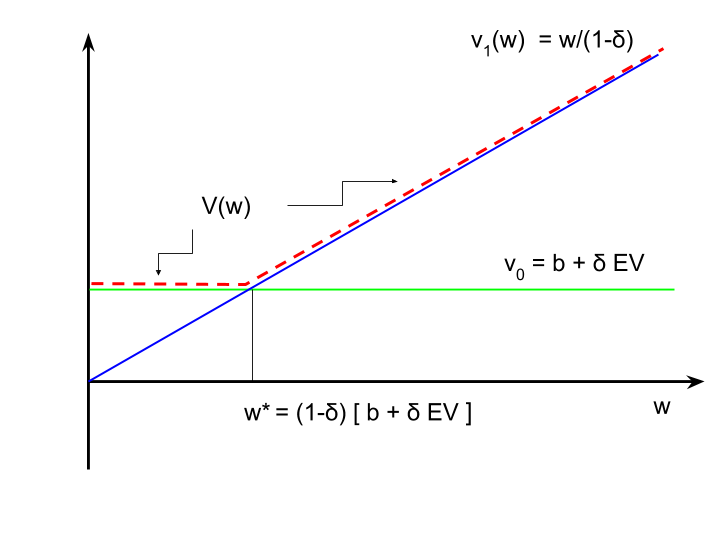
    Each period while searching a new job offer arrives with a wage $w$. If rejected then Jean has to wait until the next period to receive a new and different wage offer. This keeps happening until a wage is accepted and then the decision-making is over and Jean gets value $v_1(w)$ defined above. We now need to state the value of rejecting an offer ($a=0$). Since the wage being rejected disappears the value of rejecting it does not depend on $w,$ but it does depend on the wage offers expected to be received in the future. In particular, $$v_0 = c + \delta\,EV.$$ Here is $c$ is the utility Jean feels for not working today. This could include things like welfare payments, employment insurance benefits and other money received if not working. But it also accounts for any disutility Jean gets from working. Instead of subtracting the psychic cost of working from $w$ we add to the value of not working and include it in $c.$ You can think of $c$ as the wage-equivalent of sitting on the couch instead of going to work.

    The hard part to explain is $EV,$ which is the expected value of everything that will happen past the current page. We don't know what the number is yet, but whatever it is it does not depend on the wage $w$ rejected this period because $w$ goes away. We will derive $EV$ from the process of Jean making the right decision, in other words while maximizing value. Usually we refer to "maximizing utility." Here utility is the value associate with a single period. We then use "value" to account for preferences for all future periods as well as today.

    Jean can get either set $a=0$ or $a=1.$ The best thing is then: $$V(w) = \max\{\ v_0\ ,\ v_1(w)\ \}.$$ In other words, accept $w$ if its value is bigger than the value of rejecting it. Because $v_0$ does not depend on $w$, and because $v_1$ is increasing in $w$ we know that Jean should reject low wages and accept high ones. In fact, the optimal choice is to reject all wages with value below $v_0$. Thus, the minimum acceptable wage solves this equation: $$v_1(w^\star) = v_0.\label{ws}\tag{ws}$$ We call $w^\star$ the reservation wage. Jean should hold out until an offer arrives with $w\ge w^\star.$ The first time one does arrive take it and stop searching. We can rewrite this equation as: $$ w^{\star} = (1-\delta)(c + \delta\, EV).\label{wstar}\tag{wstar}$$ Suppose $\delta=0,$ which means Jean places no value on the future. All s/he cares about is today's utility. Then the reservation wage simply becomes $w^\star =c.$ In other words, if a wage arrives that is better than sitting on the couch take it. If $\delta>0$ then $w^\star$ will depend on $EV$.

    Before dealing with $EV$ directly, let's check whether it could be optimal for $w^\star$ to be below $c.$ According to the set up, Jean could simply plan on rejecting every wage offer forever. In this case Jean gets $c$ each period forever. Just like the PDV for a job, this results in a PDV of $c/(1-\delta).$ In other words, if $a=0$ no matter what wage was offered then $EV = c/(1-\delta).$ Further, there is no reason for Jean to do worse than this and can do better by accepting wages above $c.$ Thus, we know that in general $EV\ge c/(1-\delta).$ A little algebra on \eqref{ws} verifies: $$w^\star = (1-\delta)(c + \delta\,EV)\ \ge\ (1-\delta)(c + \delta{c\over 1-\delta}) = c.$$ In other words, even when $\delta\gt 0,$ the reservation wage will be no smaller than the value of sitting on the couch. In fact, as long as it is possible to get a wage offer bigger than $c,$ then the reservation wage will be bigger than $c.$

  2. Future Wage Offers

    3. $EV$ includes the option value of rejecting a wage. In other words, according to this model's assumptions, Jean gives up the option of accepting other wages once s/he accepts a $w.$ Rejecting a wage maintains the option of accepting a better wage that arrives in the future. Thus, rejection contains an option value that depends on what kind of wage offers are expected to receive in the future.

    Now we add the final assumption of the model. Each period the new wage offer is drawn from a distribution $F(w).$ Here $F(w)$ is the cdf of a random variable and $f(w)$ is the density. Further, these wage offers are independent over time. So the current wage doesn't tell you anything about what the next wage will be. That is important for simplicity. If wage offers were correlated over time then $EV$ could depend on the rejected wage through the correlation with future offers.

    The average offered wage is $Ew = \int_0^\infty wf(w)dw.$ (If wage offers are a discrete random variable then the expected offer would be $\sum_{i=1}^N w_f(w_i).$ Further, we assume all wages are positive because a negative wage does not make much sense in this context.) However, according to the model, Jean gets to see the wage $w$ before deciding to accept or reject it. Thus, the optional value of rejecting the wage is not simply the value $Ew.$ That would be the case if the offered wage equaled its mean value each period in the future. Then (as long as $Ew\gt c$) Jean would just get the mean wage and work at it forever. Instead, the next wage offer could be below the mean or above the mean. If it is a good wage Jean can accept it. If it is bad then Jean does not have to take it. So the value of receiving a wage offer is not the same as the value of accepting the offer. In fact, the value of the offer can be higher than the value of accepting it because rejecting the offer can have a greater value through the option value of rejection.

    You should recall that in terms of probability of events, $P(A|B) = {P(A,B)\over P(B)}.$ That is, conditional probability equals the joint probability divided by the probability of the conditioning event. If I know a roll of a dice is 4,5, or 6, then the conditional probability of it being a 4 is $(1/6)/(1/2) = 1/3.$ And the conditional probability of it being a 2 is $0/(1/2) = 0.$ THat's because the joint probability of a roll being both 2 and in the set $\{4,5,6\}$ is 0.

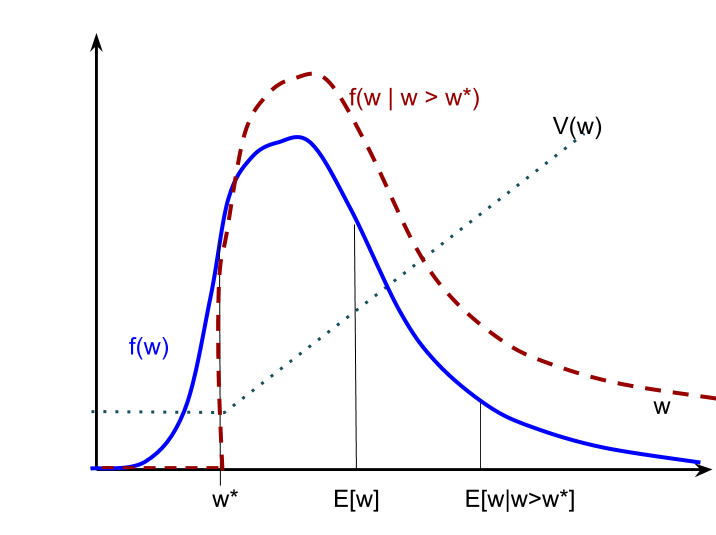
    The same logic works for conditional densities and distributions: $$f(w | w\gt w^\star ) = \cases{ {f(w) \over 1-F(w^\star)} & if $w\gt w^\star$\cr 0 & otherwise.}$$ The conditional density is pushed up by $1/(1-F(w^\star)) \gt 1.$ Then the term $E[w|w \gt w^\star]$ is the average wage knowing that it is above $w^\star.$ The conditional mean wage is $$E[ w | w\gt w^\star ] = {\int}_{0}^\infty w f(w | w \gt w^\star)dw = {\int}_0^{w^\star} w\cdot 0dw + {\int}_{w^\star}^\infty {w f(w) \over 1-F(w^\star)}dw = {1 \over 1-F(w^\star)} {\int}_{w^\star}^\infty w f(w)dw $$ Now we can use that to derive a new equation that $EV$ solves: $$\eqalign{ EV &= {\int}_0^\infty V(w)f(w)dw\cr &= {\int}_{0}^{w^\star} (c + \delta\, EV) f(w)dw + {\int}_{w^\star}^\infty {w\over 1-\delta}f(w)dw\cr &= (c+\delta\, EV) F(w^\star) + {1\over 1-\delta}{\int}_{w^\star}^\infty f(w)dw\cr & = {w^\star\over 1-\delta}F(w^\star) + {E[w|w\gt w^\star] \over 1-\delta} [1-F(w^\star)]\cr & = {1\over 1-\delta}\left[ w^\star F(w^\star) + E[w|w\gt w^\star] \left[1-F(w^\star)\right]\right].\cr} $$

    Exhibit 58. Value of Accepting and Rejecting a Job Offer

    Valueofsearch
    If Jean accepts a job with wage $w$ the present discounted value of the choice is $w/(1-\delta).$ If $w$ is rejected then $c$ is received this period and then Jean expects to receive $EV$ from the next period on. $EV$ does not depend on the wage rejected today, so whatever it is $v_0$ is flat. This means a reservation wage strategy is optimal.
  3. Solving Search as a Non-Linear System

    4. However, we are not really done yet, which is where computation comes in. The equation for $EV$ depends on $w^\star.$ And the equation for $w^\star$ depends on $EV.$ We have two equations in two unknowns but the equations are non-linear and in general cannot be solved using pen and paper. Those two equations are: $$\eqalign{ w^\star &= (1-\delta)(c + \delta\, EV)\cr EV &= {1\over 1-\delta}\left[ w^\star F(w^\star) + E[w|w\gt w^\star] (1-F(w^\star))\right]\cr}$$ We already have algorithms for solving non-linear equations (Newton-Raphson and Broyden's approximation to Newton-Raphson). We could subtract the right hand sides for both sides to express them in the form $g(x^\star)=0$ where $x^\star = \pmatrix{ w^\star\cr EV}.$ The other symbols, $c, \delta,$ and $F(w)$ are parameters of the problem.

    Exhibit 59. Offered and Accepted Wage Distributions

    AcceptedWages
    Jean draws a wage offer from $f(w)$ each search period. Wages above $w^\star$ are accepted, so the distribution of accepted wages shifts up compared to $f(w)$ so that the area between them equals $F(w^\star).$ The average (expected) accepted wage is then greater than the expected offered wage.
  4. Another Approach

    5. This problem, however, can also be solved a different way. In particular, we can start with a guess for one variable, use one equation to get the value of the other variable and then update the guess of the first variable using the second equation. It doesn't matter which variable goes first, so we might as well start with $EV$ since it appears on the right side of the first equation in the system. This idea does not always work to solve a system of equations. However, it turns out that the search model equations are special and some fancy math proves that this procedure will converge to a solution, and the solution is unique.

    Algorithm 25. Iterating on $w^\star$ and $EV$

    Given the search model with parameters $\delta, c,$ and $F(w)$ along with a method to compute $E[w|w\gt w^\star].$.
    1. Initialize.
       
      Set $EV_0$ to a number, for example, $EV_0=0.$
    2. → Compute $w^\star_t = (1-\delta)(c+\delta\,EV_t).$
      Compute $EV_{t+1} = {1\over 1-\delta}\left[ w^\star_t F(w^\star_t) + E[w|w\gt w^\star_t] (1-F(w^\star_t))\right].$
    3. Compute $\Delta = EV_{t+1}-EV_t.$
       
      If $|\Delta|\lt\epsilon$ then (convergence).
    4. Increment $t$ and repeat the previous 3 steps (go to →).
  5. Conditional Expectations
    6. The term $E[w|w\gt w^\star]$ is an expression that shows up a lot in econometrics and economic models. Here are few cases of distributions where it has a fairly simple form. For some distributions this requires numerical integration.

    Uniform Wages.
    Remember from the section on random number generators that the uniform distribution is one in which the density is a flat line. THe standard uniform is $$f(w) = \cases{ 1 & $0 \lt w \lt 1$\cr 0 & otherwise}.$$ You should be pretty easy that $E[w] = {1\over 2}.$ That is the average wage over is one-half. What happens when we condition on $w > w^\star$ (and assume $w^\star$ is also between 0 and 1? First now the range of values is not $(0,1)$ but $(w^\star,1)$. So the conditional density is $1/(1-w^\star).$ Wages are still uniform but only in the conditional range. The integration is then easy: $$E[w | w\gt w^\star] = \int_{w^\star}^1 w / (1-w^\star) dw = {1\over 1-w^\star} {w^2/2}|_{w^\star}^1 = {1 - {w^\star}^2 \over 2(1-w^\star)} = {1+w^\star \over 2}.$$ If your integration is rusty, then just remember that the anti-derivative of a linear function is quadratic. Then evaluate that at the upper and lower limits. The numerator ($1-{w^\star}^2)$) is the difference of two squares so we cancel out and get the result. The conditional mean is simply the midpoint of the range $(w^\star,1)$.

    A more general uniform distribution would take on values of $[0,U]$ where $U$ is the upper bound of the distribution. The standard uniform distribution is the case of $U=1.$ Now the density is $1/U$ and the mean wage offer is $U/2.$ Finally, the conditional mean is $$E[w | w \gt w^\star ] = {U+w^\star \over 2.}$$ Since the density is still flat these formulas are pretty easy to see and if we set $U=1$ we can verify they give the same result as the standard distribution.

    Exponential.
    Another simple distribution for solving the search model equations is the exponential distribution: $F(w) = 1 - e^{-\lambda w}$ for $w\gt 0$ and where $\lambda$ is a parameter of the distribution. It turns out that $E[w] = {1\over \lambda}$ and the integration required to show that is not too hard. It is also pretty easy to derive: $$E[w | w \gt w^\star ] = w^\star + {1\over \lambda}.$$ In words, the conditional expected wage is just the reservation wage plus the unconditional mean. So the equation for EV contains an exponential for the probabilities: $$EV = {1\over 1-\delta}\left[ w^\star (1-e^{-\lambda w^\star}) + (w^\star + {1\over\lambda})e^{-\lambda w^\star}\right] = {1\over 1-\delta}\left[ w^\star + {e^{-\lambda w^\star}\over\lambda}\right]. $$ Although there is a probability and conditional mean involved, there exponential distribution is so simple that all that is required is the exponent function to solve the problem of searching over exponential wages.

    Normal.
    The normal distribution has a somewhat more complicated expressions for this conditional mean, and deriving it is not easy. This expression is known as the Inverse Mill's Ratio (https://en.wikipedia.org/wiki/Mills_ratio). If $w\sim N(\mu,\sigma^2)$ then the truncated mean (the conditional mean given a lower bound) is $$E[w|w\gt w^\star ] = \mu + \sigma{\phi\left( (w^\star-\mu)/\sigma\right)\over 1-\Phi\left( (w^\star-\mu)/\sigma\right)}.$$ You may recall that $\phi()$ and $\Phi$ are the standard normal pdf and cdf, respectively. The ratio of the two determining the shift in the conditional mean above $w^\star.$ The expression simplifies for the standard normal distribution (when $\mu=0$ and $\sigma=1.0$): $$E[w|w\gt w^\star] = {\phi(w^\star)\over 1-\Phi(w^\star)}.$$ Unlike uniform and exponential, iteration on the search model in Ox requires use of densn() and probn(), which correspond to $\phi()$ and $\Phi()$.

    Log-normal
    Remember that a normal distribution takes on all real values, both negative and positive. So it isn't a very realistic assumption about the kinds of job opportunities someone is expecting to receive. The exponential distribution above only takes on positive values, but notice that the mode offer is 0, which again is not likely to be a good approximation to real wages. Perhaps the simplest distribution that looks more realistic is the log-normal distribution. That can be defined as the distribution of $w = e^X$ where $X$ is normally distributed, $N(\mu,\sigma^2)$. This distribution is used extensively in empirical and computational economic models. The distribution says any positive offer is possible, but the mode offer is above zero and the distribution is skewed to the right. The conditional expectation is somewhat similar to the one for the normal distribution, but it involves the ratio of the cdf and 1-cdf instead of the pdf: $$E[w|w\gt w^\star ] = e^{\mu+\sigma^2/2} {\Phi\left( (\mu+\sigma^2-\ln(w^\star))/\sigma\right)\over 1-\Phi\left( (\ln(w^\star)-\mu)/\sigma\right)}.$$

Exercises