1. Must I Paint You a Picture♭Billy Bragg 1988? Graphs in Ox

    The oxdraw module is powerful but not particularly easy to use. And the documentation does not make it easy to get started. Because Ox can save data to spreadsheet files and Stata .dta files, it is often easiest just to produce graphs using other packages. However, if your project is designed to be self-contained it might be more useful to include internally generated graphs.

    This section builds on efforts by me and past students to using graphs in Ox. In particular, only features available in Ox Console of general use are covered. It does not discuss specialized graphs or features requiring OxMetrics. http://www.doornik.com/ox/oxdraw.html or clicking on "Graphics reference" in the Ox documentation provides complete description of the package.

    Here are the primary functions for graphing data stored in vectors and matrices:
        Function          What It Does
    ----------------------------------------------------------------------------------------------
    DrawXMatrix()     plot multiple variables in a matrix against a row-vector of x values
                                  see also simpler Draw() & DrawX()
    DrawXYZ()         plot 3-D contours or surfaces
    DrawZ()           add a 3rd dimension to a XY plot
    DrawDensity()     plot a histogram of data.
    You can also add text, lines and shapes to a graph with these routines:
    DrawLine()    DrawSymbol()      DrawText()
    Finally, you can adjust the axes and other aspects of plot with:
    DrawAdjust()  DrawAxis()  DrawAxisAuto()
    Again, other functions are available, but the ones listed above will handle basic cases.
  1. Draw an Indifference Curve
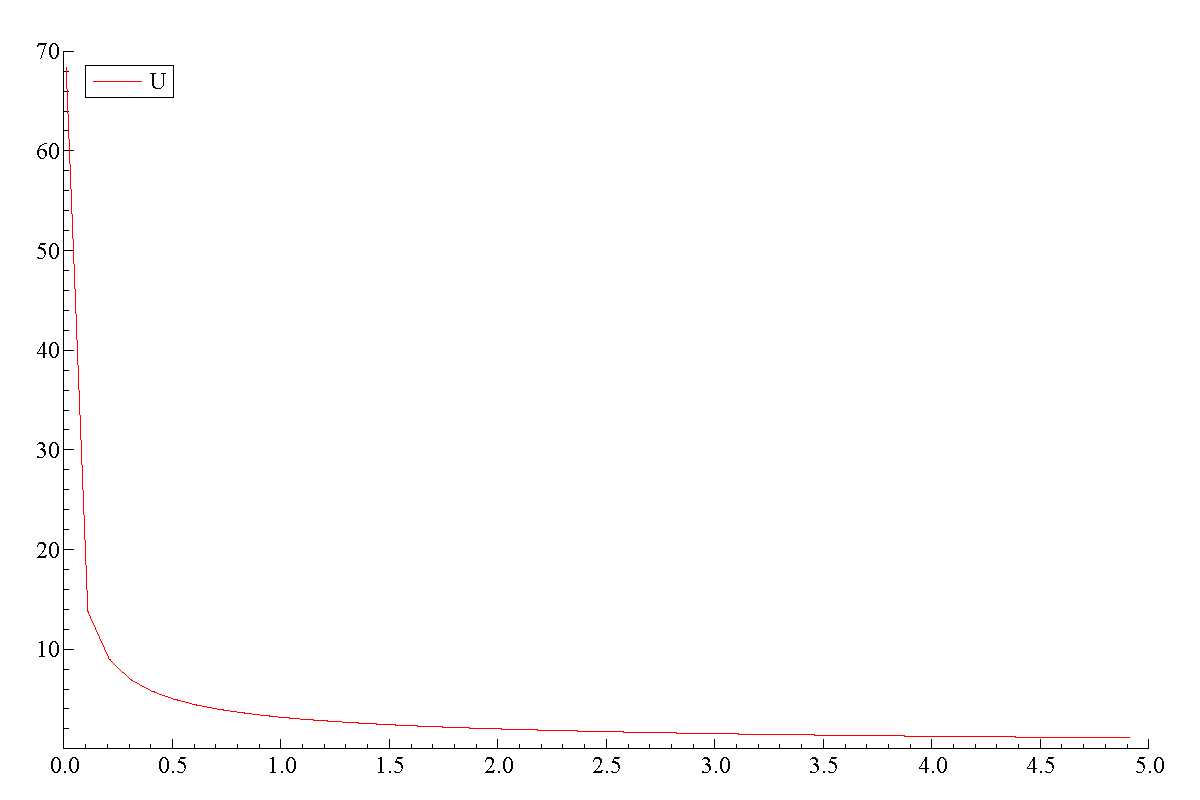
    2. To illustrate how to use oxdraw, consider the task of plotting an indifference curve for the Cobb-Douglas utility function, $U(x_0,x_1) = x_0^\alpha x_1^{1-\alpha}$. An indifference curve is the set of bundles that give equal utility: $$\left\{\ (x_0,x_1):\ x_0^\alpha x_1^{1-\alpha} = {\bar u} \right\}.\nonumber$$ The curve is defined by the number ${\bar u}$. Any combination of $(x_0, x_1)$ that yield that utility is on the indifference curve (in the set). The curve on a graph is then a function of $x_0$ that gives the value of $x_1$ that pairs with it on the curve. So we have to solve the equation above for $x_1$: $$x_1\left(x_0;{\bar u},\alpha\right) = \left[ {\bar u}/x^\alpha \right]^{1\over 1-\alpha}.\nonumber$$ To draw an indifference curve, pick a value of $\alpha$, a level ${\bar u}$ and then many different values of $x_0$ to graph $x_1(x_0; {\bar u},\alpha\bigr)$. 
    16-plot2.ox
 1:    #include 
 2:    #include 
 3:    
 4:    const decl alpha=0.4,
 5:    	        u0 = 2.1;
 6:    main() {
 7:        decl indiff, x0;
 8:        x0 = range(0.01,5,.1);
 9:        indiff = ( u0./x0.^alpha ).^(1/(1-alpha));
10:        DrawXMatrix(0, indiff,{"U="+sprint(u0)},x0,"x");
11:        SaveDrawWindow("icurve.pdf");
12:        }
    First, if you are going to draw graphs in your Ox program you have to #include "oxdraw.oxh" (line 2). We will use DrawXMatrix() in this example. The code sets $\alpha = 0.4$ and ${\bar u} = 2$. Then it generates a range of values for $x_0 = $ .01 .11 .21 .31 … 4.91. Notice that range() produces a row vector which is what DrawXMatrix expects. If you send it a column vector for $x_0$ it won't work properly.

    The program then creates the corresponding values of $x_1$ on the indifference curve, storing it in indiff, which will also be a row vector. Now we use the main graphics routine. It is easier to explain the arguments if we split them across lines: 
    DrawXMatrix(
    0,                                  // Area to draw in (0 = top left graph)
    indiff,                             // matrix to draw on the y-axis
    {"U="+sprint(u0)},                  // label(s) for each row of data
    x0,                                //  values for the x-axis
    "x"                                //  label for x
    );
    The first argument to DrawXMatrix() is 0. That means this command will affect the first graph area. You can create multiple graphs to be viewed together by drawing in areas 1, 2, 3, etc. The next two arguments are the matrix to draw followed by an array of labels to give the rows. Here we want the label to show the level of utility, so it will show U=2.1, then the x vector followed by its own label.

    At this point the graph exists internally in Ox but it won't be produced until SaveDrawWindow() is called. That means that subsequent oxdraw functions could add other things to the graph or specialize it in other ways.

    The argument sent to SaveDrawWindow is the name of the file. Since the extension is .pdf the file is saved as PDF. The other formats that Ox Console will save to are probably not useful to you. This is one of the limitations of the free version of Ox. The professional version allows you to view graphs interactively and to save them to image formats by copying it the clipboard.

    Exhibit 24. An Indifference Curve

    Suppose we wanted to view not just the line but the evaluated points at each pair of points as well. We can do that by adding one of the optional arguments to DrawXMatrix instead of using the default value. Namely: 

        DrawXMatrix(0, indiff, {"U="+sprint(u0)}, x0, "x", 2 );
                                                       ↑
    The final "2" is the optional argument that was not sent above, so the default value of "0" was used. That argument sets the plotting style for the graph. Another way to write this is to use the "tag" for that kind of style: 
        DrawXMatrix(0, indiff, {"U="+sprint(u0)}, x0, "x", ST_LINESYMBOLS);
                                                       ↑
    This use of integers or aliases (tags) for those integers to change the plotting options is one feature of oxdraw. It is not easy compared to a menu-driven system, but it is very easy to make sophisticated graphs within a program.

  2. Three-Dimensional Graphs
    3. Sorry ... not done

Exercises